Главная | О сайте | Задачи | Проекты | Результаты | Диверсификация | Новости | Вопросы | История | Информация | Ссылки
Космическая погода на текущий час
Войти / Регистрация
Секция Совета РАН по космосу
Красные карлики и «дихотомия Кеплера»
По данным, полученным космическим телескопом им. Кеплера, у звезд красных карликов в среднем по 4-8 планет, орбиты которых наклонены друг к другу на 0-6°.
Владислава Ананьева
Сара Баллард (Sarah Ballard) из Вашингтонского университета и Джон Ашер Джонсон (John Asher Johnson) из Гарвард-Смитсоновского центра астрофизики провели статистический анализ планетных систем Кеплера, принадлежащих красным карликам. Их интересовал вопрос, распространяются ли статистические закономерности строения планетных систем, подмеченные для солнцеподобных звезд, на более легкие и более многочисленные М-карлики? Как оказалось – да.
Миссия «Кеплер» была посвящена поиску планет у солнцеподобных звезд. Красных карликов среди целевых звезд на поле Кеплера было всего около 5500 из более чем 160 тысяч, т.е. менее 4%. Тем не менее, обнаруженного количества транзитных кандидатов у этих звезд оказалось достаточно, чтобы можно было делать определенные выводы.
Баллард и Джонсон отобрали из каталога транзитных кандидатов Кеплера (KOI) 167 надежных кандидатов, вращающихся вокруг 106 звезд, чья температура была ниже 4200К, т.е. спектральных классов от K7 V до M4 V. В их выборке оказалась 71 однопланетная система (с одним транзитным кандидатом), 17 двухпланетных, 12 трехпланетных, 4 четырех планетных и 2 пятипланетные системы (Kepler-32 и Kepler-186). Они построили синтетическую популяцию планетных систем с различным количеством планет в одной системе и разным взаимным наклонением орбит планет, и попытались определить, какая из популяций будет больше всего напоминать наблюдаемое распределение планет Кеплера.
Как и исследователи планетных систем у солнцеподобных звезд, Баллард и Джонсон столкнулись с эффектом, получившим название «дихотомия Кеплера». Этот эффект заключается в том, что совокупность наблюдаемых планетных систем нельзя описать одним-единственным распределением: количество однопланетных систем оказывается примерно в 2 раза больше, чем должно быть, исходя из видимого количества двух-, трех- и еще более населенных планетных систем. Это означает, что помимо плоских многопланетных систем, количество транзитных кандидатов в которых определяется углом наклона средней плоскости системы к лучу зрения, существует значительная популяция однопланетных систем (или же систем, орбиты планет в которых значительно наклонены друг к другу).
Если попытаться решить задачу «в лоб» и попробовать подобрать единое распределение планетных систем по числу планет и взаимному наклонению орбит, то «средняя» система у звезды красного карлика будет иметь 6 ± 2 планет, а их орбиты окажутся наклоненными друг к другу на 7.4 +2.5/-4.6°. Но такое распределение явно занижает количество однопланетных систем и завышает – двухпланетных.
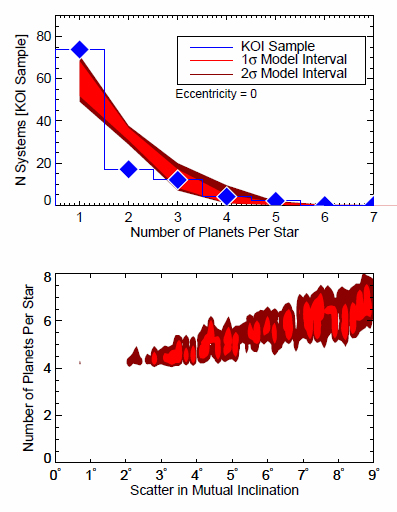
- Зависимость количества планетных систем от числа планет в одной системе. Синими ромбами показаны наблюдательные данные, красной полосой – предсказания наилучшей "однородной" модели. Видно, что "однородная" модель занижает количество однопланетных систем и завышает количество двухпланетных.
Однако если рассматривать только многопланетные системы (т.е. те, в которых есть два или больше транзитных кандидатов), картина заметно меняется. В этом случае ожидаемое количество планет у одной звезды становится больше 5, а взаимное среднее наклонение орбит уменьшается до 4.6 +1.7/-3.0°.
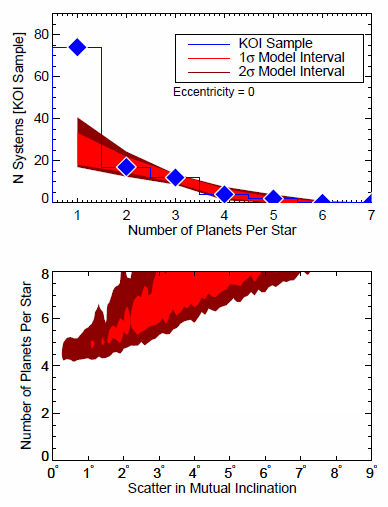
- Зависимость количества планетных систем от числа планет в одной системе. Синими ромбами показаны наблюдательные данные, красной полосой – предсказания модели, описывающей только многопланетные системы. Виден наблюдаемый избыток однопланетных систем.
Авторы исследования рассмотрели модель, в которой совокупная популяция планетных систем состоит из двух подмножеств: «однопланетных» систем, и многопланетных систем с небольшими углами наклона орбит планет друг к другу. Также они учли влияние не равных нулю эксцентриситетов орбит. Такая «составная» модель описывала наблюдаемое распределение транзитных кандидатов Кеплера гораздо лучше, чем рассмотренная ранее модель с «единым для всех» распределением.
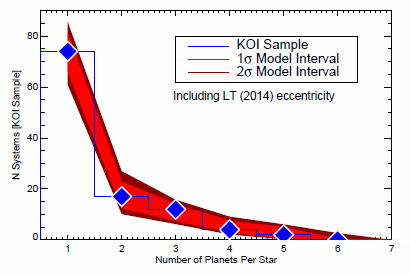
- Предсказания "составной" модели близки к наблюдательным данным.
Окончательно, общая картина выглядит так. Согласно анализу, проведенному Баллард и Джонсоном на основе данных Кеплера, планетные системы M-звезд бывают двух видов, «однопланетные» и многопланетные. Доля однопланетных систем оценивается в 55 +23/-12%. В среднем на каждую M-звезду приходится 6.1 ± 1.9 планет, причем их орбиты наклонены друг к другу на 2 +4/-2°. Авторы не раз оговариваются, что «однопланетность» однопланетных систем не надо понимать буквально – скорее всего, в этих системах планет тоже несколько, но их взаимные наклонения орбит достаточно велики, так что транзитной там оказывается только одна планета. Возможно, корректнее было бы называть однопланетные и многопланетные системы «динамически горячими» и «динамически холодными».
Замечу, что Солнечная система с точки зрения «Кеплера» также является однопланетной, т.е. «динамически горячей». Наклонение орбиты Меркурия к эклиптике составляет 7°, Венеры – 3.4°. Поэтому если некий аналог «Кеплера» наблюдал бы Солнечную систему издалека, он обнаружил бы или транзиты Меркурия, или транзиты Венеры, но не их обоих вместе.
Интересно, что свойства родительских звезд «динамически холодных» и «динамически горячих» систем несколько отличаются друг от друга. Средняя металличность звезд с «динамически холодными» системами оценивается Баллард и Джонсоном в -0.09 ± 0.04, а «динамически горячих» – в -0.03 ± 0.02. Звезды «динамически холодных» систем чуть быстрее вращаются вокруг своей оси (средний период вращения таких звезд 19 ± 1.4 суток, а у звезд с «горячими» системами – 21.7 ± 1.3 суток). Также «многопланетные» системы в среднем несколько выше поднимаются над галактической плоскостью, чем «однопланетные». В чем причина этих различий, еще предстоит выяснить.
Источник: http://arxiv.org/pdf/1410.4192.pdf
Комментарии
Комментарии
Вертикальная линия. Она пересекает небесную сферу в точках зенита и надира. Как следует из ее названия... [далее]
Сайт разработан и поддерживается лабораторией 801 Института космических исследований Российской академии наук.
Подбор материалов - Н.Санько
Полное или частичное использование размещённых на сайте материалов
возможно только с обязательной ссылкой на сайт Секция Солнечная система Совета РАН по космосу.